데이터 사이언스를 위한 통계학 입문(2주차)
✓ 2주차 빅데이터 탐색의 첫걸음 ✓
2주차 1강 《데이터의 평균 - 중심 위치》
✓ 평균 : 하나의 값으로 표현한 요약된 정보(추정치)
평균 공식 : 데이터값의 총합을 데이터의 갯수로 나눈 것
모든 데이터를 일일이 나열할 필요 없이 평균을 통해 하나의 값으로 요약된 정보를 쉽게 접할 수 있다.
“평균은 혼자 존재하는 개념이 아니다!”
* 평균과 표본 선정 : 표본 선정을 어떻게 하느냐에 따라 평균값에 영향을 미치게 된다. 표본 샘플이 알아보고자 하는 데이터를 포괄할 수 있어야 알아보고자 하는 값을 보다 정확하게 알 수 있다.
✓ 평균을 다룰 때 주의해야 할 점
평균값이 정확하기 위해서는 적합한 표본을 선정하여야 한다. 반복적으로 실험할 때 유사한 값이 나오고, 기대값과 비슷할수록 적합한 표본이라고 말할 수 있다.
“조사된 평균값이 모집단을 대표하는 통계치라고 할 수 있는가?”
→ 이를 위하여 모집단의 특징을 대표할 수 있는 표본을 선정하는 것이 중요하다.
표본이 적합하게 추출되었는지 평가하는 방법
- 편의가 적은가? : 표본으로부터 얻어지는 통계치의 기대값이 모수의 참값과 유사한가?
- 정확도가 높은가? 반복하여 표본을 추출할 경우 얼마나 유사한 값들이 나오는가?
* 평균과 분산 : 같은 평균이라도 분산이 다르면 데이터 특성은 다르다
* 평균값은 그 집단에서 가장 많이 존재하는 값이 아니다 ☞ 중심값일 뿐, 평균값에 해당하는 표본이 가장 많이 존재한다고는 생각할 수 없다.
✓ 데이터의 중심 척도 요약
평균은 표본이 적은 경우 아주 큰 값이나 작은 값에 민감한 추정치이다. 때로는 중앙값이 평균보다 더 적합한 중심척도인 경우도 있다.
- 중앙값 : 관측치를 크기순으로 배열했을 때 중앙의 위치에 놓이게 되는 값
데이터의 수가 적고 이상치가 있을 때 평균보다 더 정확한 모집단의 중심값이 된다.
- 최빈값 : 전체 데이터 중 가장 빈도가 높은 값. 데이터의 수가 많아질수록 평균과 가까워진다.
2주차 2강 《데이터의 분산 - 산포 정도》
“평균만 제공될 때와 평균과 표준편차가 제공되는 경우, 해석할 수 있는 정도가 다르다!”
데이터의 산포는 그래프로 그렸을 때에 더 잘 알아볼 수 있다. 히스토그램을 통해 데이터의 산포 정도(분산)을 알아볼 수 있음.
데이터의 산포 정도가 크다는 것은 무엇을 말하는 것일까?
⑴ 그래프를 확인했을 때 데이터가 중간에 몰려 있지 않고(평균값과 가까운 값이 적고) 멀리 퍼져 있다.
⑵ 많은 데이터들이 중심 위치(평균값)로부터 멀리 떨어져 있다.
⑶ 데이터의 평균과 데이터들의 차이가 크다.
✓ 데이터의 평균과 데이터들의 거리의 합을 통해 분산을 계산할 수 있다.
데이터가 평균으로부터 대칭적으로 존재할 경우 편차들의 합이 0이 된다. 그래서 편차를 제곱하여 더하면 됨.
분산 : 편차들의 제곱합을 (n-1)로 나눈다
☞ n-1로 나누는 이유: 자유도와 관련하여 평균값으로 표본 평균을 사용하기 때문에 1개의 자유도를 잃게 되어서 n-1임.
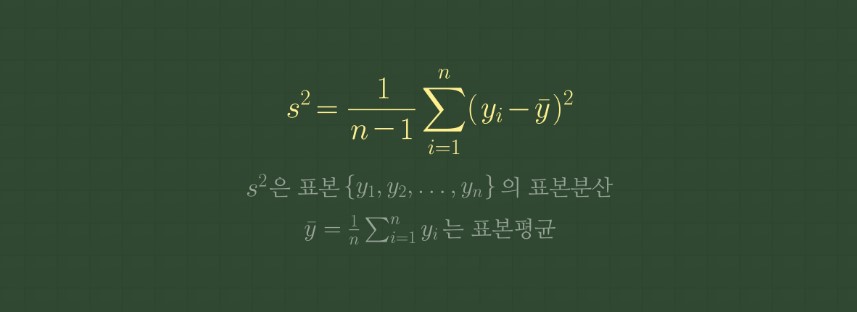
✓표준편차 : 개별데이터값-평균값의 차이를 제곱하여 더했으므로 값이 커지고 단위가 달라진다. 분산에 제곱근을 취해 원래 단위로 복원한 것이 표준 편차이다.
✓ 분산: 데이터가 분포되어 있는 정도.
분산값은 평균값만으로는 데이터를 상상하기 어려운 상황에서 데이터에 대한 요약정보를 보완해준다.
평균은 높으나 표준편차가 높다면 값들 사이의 격차가 매우 크다는 것을 알 수 있다.
'데이터 과학 · 정보 통계' 카테고리의 다른 글
| [포스텍 MOOC] 데이터 사이언스를 위한 통계학 입문(1주차) (0) | 2019.12.12 |
|---|